New algorithm for Mie scattering coefficient (2)

1.New algorithm of an and bn

In order to solve the above problems, the author proposed a new algorithm. Transform the formulas of an and bn as follows: Let

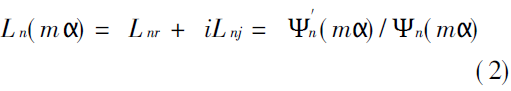
Among them, Lnr and Lnj represent the real part and imaginary part of Ln(m) respectively. Substitute equation (2) into equation (1), and use anr, anj and bnr, bnj to represent the real part and imaginary part respectively. So it can be deduced.

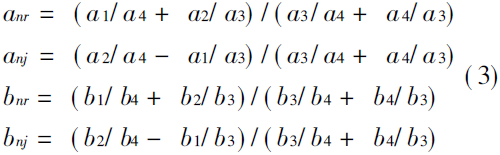
It is very important to use the form of ratios in the four formulas, so as to avoid important overflows that may occur when ai and bi increase in the delay push process. This is an important feature of the algorithm mentioned above. Among the above four formulas.

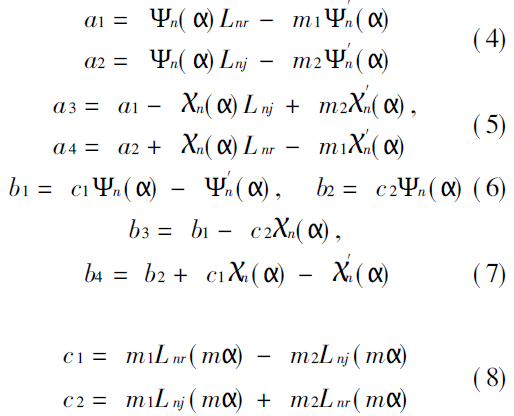
Since 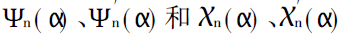are all functions of real variables,The calculation does not produce overflow. The key is how to deal with the algorithm of  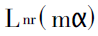and 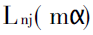  .This ensures that no overflow occurs during calculation. In Lentz's algorithm, a continued fraction is used to calculate the value of Ln, and its accuracy is guaranteed by obtaining an empirical formula for the number of truncated terms N and parameters a and m based on a large number of calculations. Such an empirical formula has practical limitations on the one hand, and it will also bring truncation errors on the other. Literature (6) has improved this empirical formula, but it is still stuck in the range of a=1~100, m1=1~2, m2=0~1. The following introduces the new algorithm for Ln developed by the author of this article. The characteristic of this algorithm is that it is not limited by the values of a and m, does not produce pathological phenomena such as overflow or non-convergence, and has a fast calculation speed.

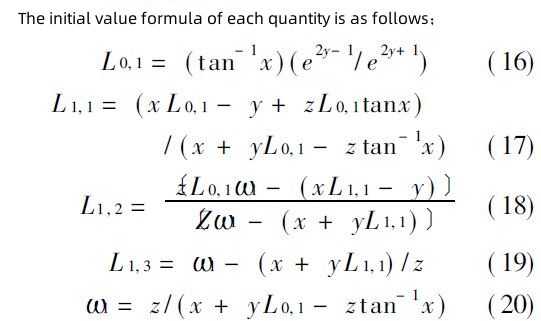
The equations (3) - (20) derived above constitute the complete algorithm of Mie coefficients an and bn. Since an and bn are calculated starting from n = 1, the values of an and bn of any series can be calculated using the initial value formulas (16) - (20), so there is no problem of rounding error. It can be seen from equation (16) that because y= m2ɑ≤0, no matter what values m2 and ɑ take, there will be no overflow. In addition, the formulas in (3) adopt the form of ratios, which avoids the need for calculations. overflow, which fundamentally solves the overflow problem.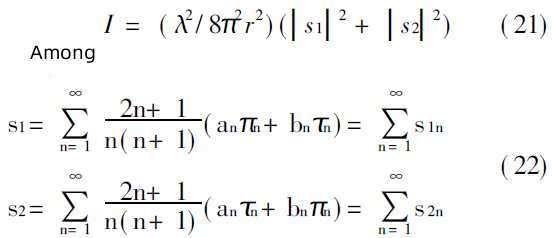

Ξ is the minimum data limit of the computer in double precision.

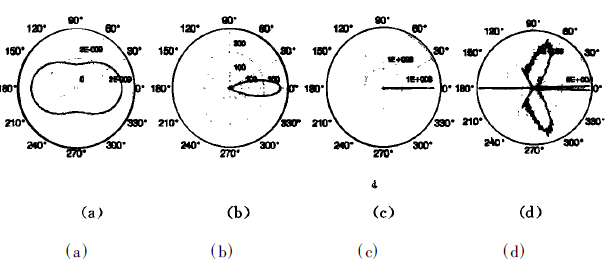
Figure 1 shows a set of calculation examples of scattered light intensity. Among them, m1=1.33, m2=-0.4, and λ=0.6328 correspond to the particle diameters of d=0.001, 1.0, and 30 μm respectively. The picture d is a partial enlargement of the scattering pattern when the particle diameter d=100μm. It can be seen that as the particle size increases, forward scattering rapidly strengthens and complex side lobes appear.

Changes in real part (a) and imaginary part (b). It can be seen that with the increase of m1 and m2, although the size of the particles remains unchanged, the scattering is also strengthened, and the backscattering is strengthened with the increase of m1 and m2.

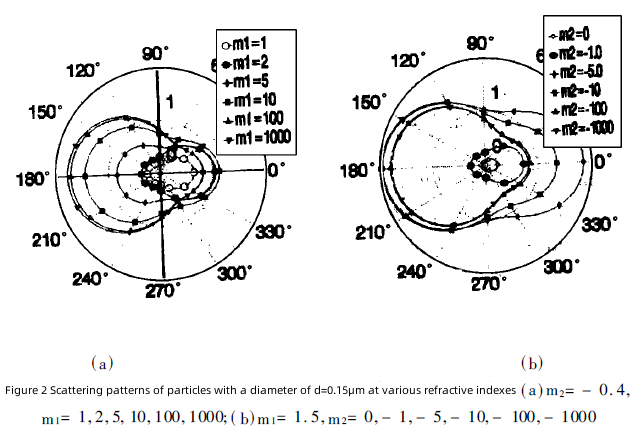
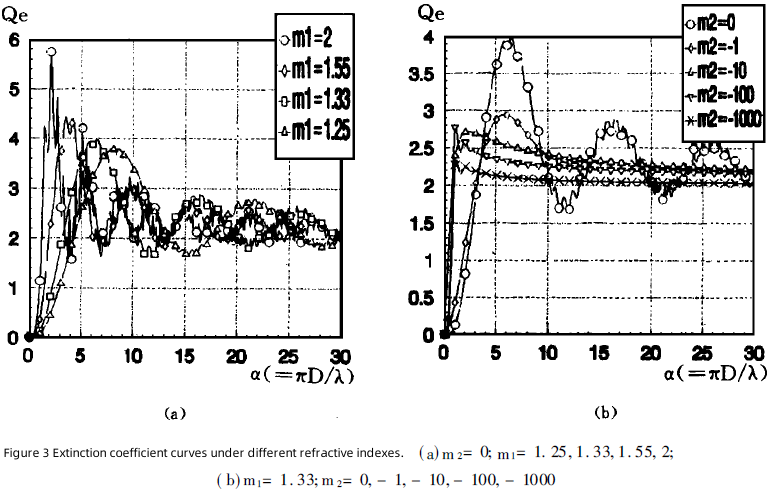
Figure 3 shows the calculation results of the extinction coefficient, where a) and b) represent the changes of the extinction coefficient with the real part and imaginary part of the refractive index respectively. It can be seen that as the particle diameter increases, the extinction coefficient approaches 2; the increase in the refractive index, especially the increase in the imaginary part of the refractive index, makes this approach faster and more obvious. In addition, when the imaginary part of the refractive index m2=0, the extinction coefficient oscillates as the particle diameter increases; but when m2≠0, the oscillation disappears quickly.

The value of FM(Z) corresponding to the maximum light intensity is determined by the above formula. It can also be seen from the above formula that the focal shift size in this limit case is mainly determined by S0/f and Na.