New algorithm for Mie scattering coefficient (1)

1. Introduction

Mie theory is a strict analytical solution to the particle size distribution of desert light [1]. It is currently widely used in engineering and technical fields such as environmental protection, power, meteorology, astronomy, two-phase flow, and powder particle distribution measurement. Measurement data of the light scattering field of a particle or particle group. Many physical properties of particles or particle groups can be deduced inversely, such as particle size, particle refractive index, etc. [2]. However, the inverse calculation must be calculated in advance. In 1968, Dave[3] first published the complete Mie filter calculation method, and then Lentz[4] and Wiscomb[5] proposed partial calculations. New algorithm. Some people in China have also published their own algorithms [6, 7, 8]. But in general, these algorithms have their own size limitations. Especially when the imaginary part value of particles or pixels increases, the calculation speed is often too slow or overflow and non-convergence occur. The phenomenon paper introduces the new algorithm of Mie converter developed by the author. The size characteristic of this algorithm is that it is not limited by particles and pixels, does not cause overflow and non-convergence, and has a fast calculation speed.

2. Calculation formula of Mie coefficient

The central problem of Mie coefficient calculation is to calculate the Mie coefficient coefficients an and bn, and their expressions are [9].

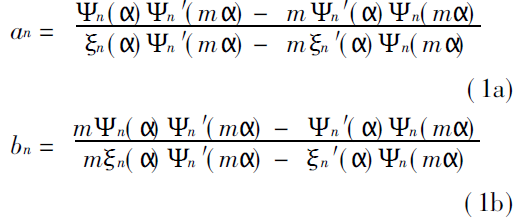
where is the size parameter of the particle, defined as α=πd/λ, d is the diameter of the particle, λ is the wavelength of the incident light in the medium surrounding the particle, and m is the relative complex refractive index of the particle in the surrounding medium, that is, m= m¹ + im² ( m²< 0)

, where i is the imaginary unit. The expressions of Ψn( Z) and ξn( Z) (Z represents both α and mα) are 

                                                                                                Ψn(Z)=（πZ/2）Jn+1(Z)

                                                                            Ψn(Z)=Ψn(Z)+iΧn(Z)

                                                                                  Χn(Z)=  ̶ (πZ/2)( ̶ 1)n-1J-(n-1)(Z)

                                                                                                    =   ̶ (πZ/2)Nn+1(Z)

3. Causes of overflow in calculations

To calculate the Mie coefficient, you must first calculate Ψn and Χn. The recursive method is generally used. Recursion is divided into forward recursion (that is, starting from n = 0) and rigid recursion (that is, starting from n = N to n = 0, N is the preset value). Experiments show that forward push is always faster than rigid push. Initial values of Ψn and Χn

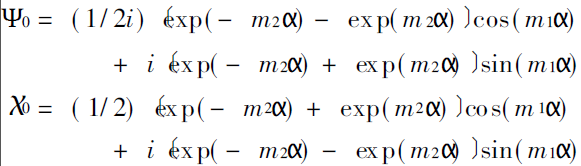
From the analysis of the above two equations, it can be seen that when m₂≠0, if the particle size d is very large, or the imaginary part value m₂ of the complex refractive index is very large, the product m₂ d will be very large, which can make the term exp(- m₂ α in the two equations ) =exp ( - π m₂d/ λ) The value exceeds the data limit of the computer, resulting in overflow. This is an important reason for overflow. In addition, inappropriate algorithms may also cause overflow during the recursion process.